Scales: Complexity built on simplicity: 576+ scales from 6 sets of 3 intervals

576+ scales from 48 diatonic scales as modes of 16 basis scales from 6 tetrachords

by Kevin Ferguson

Here's a strategy to quickly master all 7 note scales which have 7 unique scale degrees. These cover the western classical modal scales (based on tempered scales) as well as the 10 classical Hindustani that's (based on pure harmonics), a large set of important components of the Turkish, Arabic and related Maqam, and many others. And even mores scales, including blues scales, correspond to extended modes some of of these 48 scales.

I derived the 16 Basis Scales in 2006 using concepts of basis vectors for transforms applied to the 48 heptatonic scales. I've been using these and their modes, which span the 48 scales since then in performances and my recordings of hundreds of world music, original music and, especially lately, improvised music. As of 2012, I perform regularly with Playback Theater, an improve theater group that listens to audience member stories and plays them back on the spot as improvised performances accompanied by music I improvise. Having a wealth of scales and the theory behind them at your finger tips comes in handy for this.

The approach I'm taking here is to take small intervallic building blocks to build a set of basis scales, of which modes span a complete set of scales. That is, we'll use 4 note interval building blocks, 4 on the bottom and 4 on the top for 8 notes covering 1 octave, to construct 16 unique scales. Modes of a scale correspond to moving the tonic from the first note in the scale to the second, third, forth, fifth, sixth or seventh. Using modes of the 16 basis scales, we can create the 48 scales. All of this is done using relative intervals such that transposing each of the 48 scales across the chromatic scale gives us 576 scales to work from. And even mores scales, including blues scales, correspond to extended modes some of of these 48 scales. But wait, there's more: using concepts from Maqam and other music paradigms, scales can be constructed that change from octave to octave, so that an extremely large number of scales can be created....But let's start with looking at 4 notes at a time, or more specifically 3 relative intervals of 4 notes.

Tetrachords

Tetrachords are a set of 4 notes. The intervals between these 4 notes identifies what kind of tetrachord these 4 notes construct. For example, C,D,E,F is a major tetra-chord with successive intervals being whole note (between C and D), whole note (between D and E) and half note (between E and F). In terms of chromatic (half note) steps, the corresponding intervals are 2, 2 and 1. Likewise, a minor tetra-chord is made up of 4 notes whose relative intervals correspond to the first 4 notes in a minor scale. An example of a minor tetra-chord is C,D,Eb,F with respective successive intervals being whole, half, whole: 2, 1, 2. So tetra-chords can be classified by 3 successive intervals. Here are the 6 tetra-chords that are required to build the 16 basis scales used to create the 48 heptatonic scales:


-----------------------------------------------------------------------------------------------------

				  6 Basis Tetra-chords

-----------------------------------------------------------------------------------------------------
  		    |		 Intervals
  Name        	    |--------------------------------------------------------------------------------
        	    |	  Steps		Type of 2nd		Number of chromatic steps
-----------------------------------------------------------------------------------------------------
  Minor 	    | 1, 0.5, 1: 	major, minor, major: 		2 1 2
  Major 	    | 1, 1, 0.5: 	major, major, minor: 		2 2 1
  Phrygian 	    | 0.5, 1, 1:  	minor, major, major: 		1 2 2
  Major Phrygian    | 0.5, 1.5, 0.5: 	minor, augmented, minor:	1 3 1
  Todi   	    | 0.5, 1, 1.5: 	minor, major, augmented: 	1 2 3
  Purvi (Major Todi)| 0.5, 1.5, 1:	minor, augmented, major: 	1 3 2

Lower Tetra-chords

Lower tetrachords define the first 4 notes of the scale. For example, C major scale starts with a major tetrachord. The lower tetrachords of the 16 basis scales include all 6 of the basis tetrachords listed above.

Upper Tetra-chords

Upper tetrachords define the second 4 notes of the scale. For example, C major scale continues after the first 4 notes (starting on the 5th note, G) with a major tetrachord. The upper tetrachords of the 16 basis scales include only 4 of the 6 basis tetrachords listed above: minor, major, phrygian and major phrygian. So, in other words, the 16 basis scales do not use todi or purvi for upper tetrachords.

Combining Lower and Upper Tetrachords to Create The 16 Basis Scales

Now we combine the lower and upper tetrachords in a way that gives us the 16 Basis Scales. Again, the example of the major scale uses major for the lower and upper tetrachords. Ascending melodic minor (e.g. C,D,Eb,F,G,A,B,C ) uses a minor lower tetrachord (C,D,Eb,F) and a major upper tetrachord (G,A,B,C). Likewise, we can construct all 16...

16 Basis Scales


-----------------------------------------------------------------------------
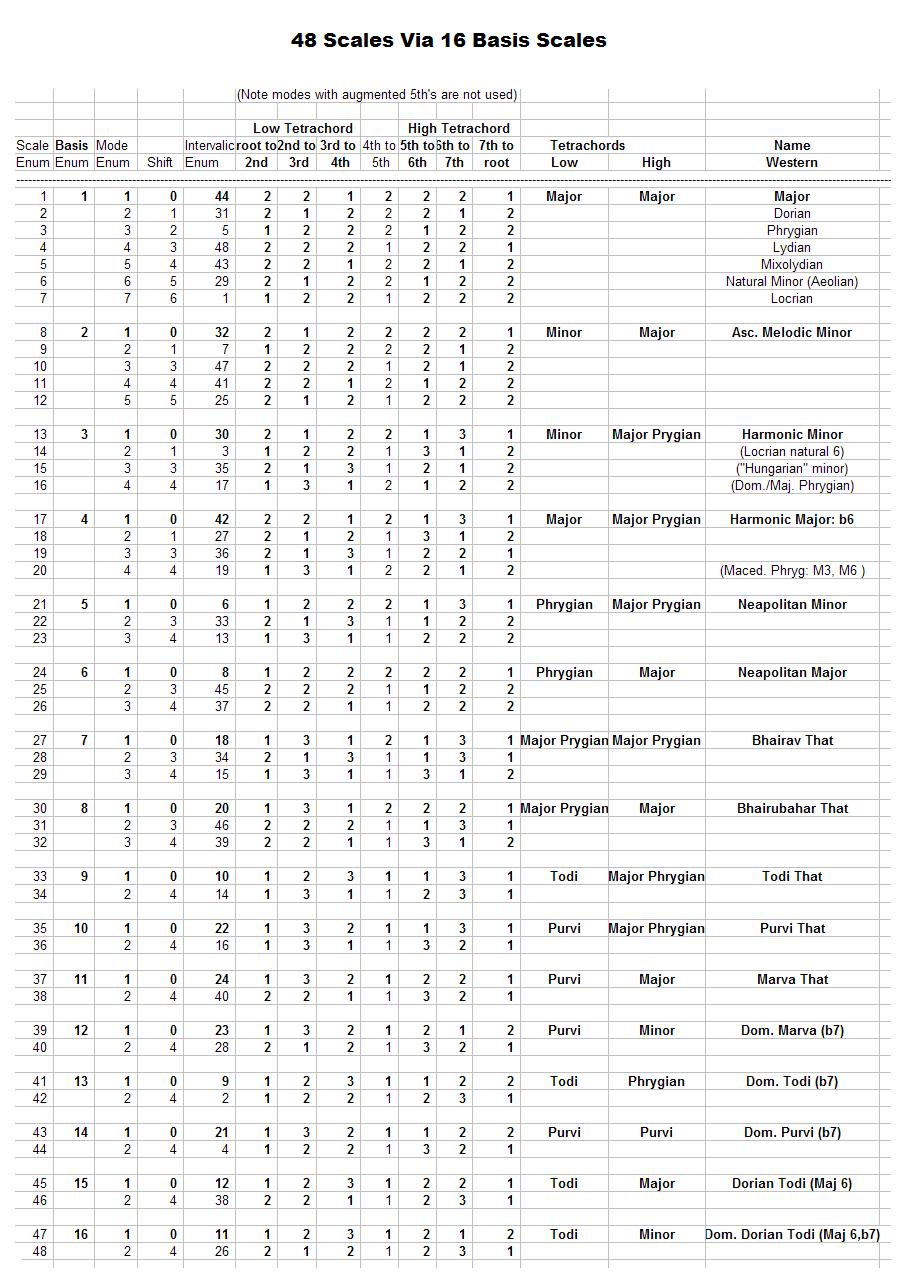
			16 Basis Scales
-----------------------------------------------------------------------------
Basis			Lower		Upper		Example using C as 
Scale			Tetrachord	Tetrachord	     the tonic
-----------------------------------------------------------------------------
Major			Major		Major		C D  E  F  G A  B  C
Ascending Melodic Minor	Minor		Major		C D  Eb F  G A  B  C
Harmonic Minor		Minor		Major Phrygian	C D  Eb F  G Ab B  C
Harmonic Major		Major		Major Phrygian	C D  E  F  G Ab B  C
Neapolitan Minor	Phrygian	Major Phrygian	C Db Eb F  G Ab B  C
Neapolitan Major	Phrygian	Major 		C Db Eb F  G A  B  C
Bhairav			Major Phrygian	Major Phrygian	C Db E  F  G Ab B  C
Bhairubahar		Major Phrygian	Major 		C Db E  F  G A  B  C
Todi			Todi		Major Phrygian	C Db Eb F# G Ab B  C
Purvi			Purvi		Major Phrygian	C Db E  F# G Ab B  C
Marva			Purvi		Major 		C Db E  F# G A  B  C
Dominant Todi		Todi		Phrygian	C Db Eb F# G Ab Bb C		
Dominant Purvi		Purvi		Phrygian	C Db E  F# G Ab Bb C
Dominant Marva		Purvi		Minor 		C Db E  F# G A  Bb C
Minor Marva		Todi		Major		C Db Eb F# G A  B  C
Minor Dominant Marva	Todi		Minor		C Db Eb F# G A  Bb C

The 48 Diatonic (Heptatonic {7 Tone}) Scales

There are 48 possible diatonic/heptatonic unique scales that can be created using major or minor 2nd, 3rd, 6th and 7th scale degrees plus either perfect or augmented forth and either diminished or perfect 5th (with no overlap of augmented 4th and diminished 5th). These 48 scales can be enumerated directly simply by starting with all major and perfect intervals (the major scale) and then changing each interval one by one until all possible combinations have been used. Alternatively, modes of the 16 basis scales can be used to form the same 48 scales. Just as minor is a mode of major, where the 6th note of the major scale is used as the tonic for the minor scale (e.g. for C major {C D E F G A B C}, the corresponding minor mode is A minor {A B C D E F G A }, modes of the 16 basis scales together include all 48 diatonic scales.

The table below shows the 48 scales as modes (indicated by the "Shift" column which corresponds to how many scale degrees to skip to find the tonic of the mode vs. the basis scale).

More scales

And even more scales can be derived directly from these 48. For example, common 7 note blues scales based on pentatonic scales with "chromatic accidentals" placed between the two pairs of notes with whole step intervals correspond to a "mode" of Purvi (and Indian "that"): the 2nd note of Purvi corresponds to the first of the minor blues scale. The mode using the 3rd note of Purvi as the tonic corresponds to the major blues scale with accidentals between intervals with major 2nds. Note that these blues scales are not included in the 48 diatonic scales we have earlier defined because both violate the rule that each scale degree must be unique (e.g. the minor blues scale example has neither a major nor minor 2nd scale degree and likewise it lacks the 6th scale degree, these being substituted with the augmented 4th between the perfect 4th and perfect 5th and the major 7th between the minor 7th and octave).

Add trajectory rules and the possibilities are practically infinite

In western classical (pre-Baroque through post-Romantic, but especially in Baroque) music, melodic minor was often used. Melodic minor uses the melodic minor scale when ascending and the natural minor (commonly known as just "minor") scale when descending. Hindustani classical raags (ragas), there are many examples of much more complex alterings of scales depending on how far one has traversed the scale and other similar rules. Both Hindustani classical and Maqam (Turkish, Arabic and similar) music often alter scales depending on which octave the melody lies.

So, using the 6 sets of 3 intervals to form tetrachords from which to form the 16 basis scales, which in turn form the 48 scales, which can each be played using 12 tonics (on western instruments), and further modified based on scale direction, degree, octave and the location in the progression of the melody, one can has a nearly infinite set of melodic possibilities from which to choose.

Kevin Ferguson is a Portland, Oregon based guitarist, engineer, scientist, inventor with several albums and dozens of patents. See his homepage for more articles on music, including how to master complex rhythms and example audio and video recordings of his performances of these using many of the scales described above, along with music videos, inventions and more.

Additional Columns by Kevin Ferguson

Mownky!