Mastering Odd, Complex Time Signatures And Rhythms

by Kevin Ferguson w/

Featured example tune:

© 2008,2020 Kevin Ferguson/Debone Music

Growing up, the progressive rock and jazz/rock fusion tunes I'd play would sometimes bewilder those in the mood to dance. How could anyone possibly dance to such odd and complex rhythms and changing time signatures? Some of the more famous and simple versions of these include the theme for the TV series and movies "Mission Impossible" (in 5/4), "Take Five" (5/4) and Pink Floyd's "Money" (7/4).

Ironically, in music from other parts of the world, many of the odd and quite complex time signatures, rhythmic meters and patterns are actually derived from the rhythm of the dance the music was developed around. For example, in the southern Balkans (Macedonia, Bulgaria and to a lesser extent in Greece), one finds time signatures such as 5/8, 7/16, 11/16 and combinations such as 25/16 (7/16:11/16:7/16) [2].

Here's an approach to

This approach can also be applied to many syncopated rhythms in more familiar time signatures. For this, I also give some examples of rhythms from Salsa, Flamenco and West African music. I explain a simple way to think of them and associated ornamentation and give audio clip examples from fiery folk tunes I've learned from the cultures that created them. Most of the audio clips are from my "Exotic Extremes" CD.

Galloping Apples

After studying the music for a while, learning some tunes and playing with musicians much more experienced than I at the time, the biggest breakthrough in being able to internalize the rhythms came from learning the associated folk dance. Balkan dance rhythms were taught to me using the rhythm of words to denote long and short duration steps.

For example, "apple" is used for short steps spanning 2 beats, such as 2 sixteenth notes, and "galloping" for long steps spanning 3 beats. Then rhythms are assembled with the correct stressed or accented beats by the correct choice of combinations of 2's and 3's: "apple apple galloping" is a 7/16 rhythm with accents at the first beat of each of groups of 2, 2 and 3, counted as "1 2 1 2 1 2 3":

Example audio of a fast (about as fast as it is possible to count the beats out loud) example of this 7 beat rhythm and time signature include:

Likewise, another form of 7/16 is 3, 2, 2, represented with "galloping apple apple":

Middle Eastern and Northern Indian (Hindustani) Classical also use the idea of assembling 2's and 3's to construct rhythm [3]. Hindustani rhythmic cycles are known as tal or tala. Examples include "jhaptal" with 10 beats and "rupak" also with 7 beats [1]. 

	Jhaptal: 2+3+2+3 = 10 beats
	Rupak: 3+2+2 = 7 beats

Borrowing from the Balkan dancer method, this would be: 

	Jhaptal: "apple galloping galloping apple" Rupak: "galloping apple apple"

Typically, both jhaptal and rupak would be much slower than the Balkan equivalent, so try saying the above apples and gallopings in slow motion to get a feel for the typical average tempo of these Hindustani rhythmic cycles.

In these examples, the words "apple" and "galloping" convey the rhythmic pattern and also aid in memorization. The memorization aid aspect has lead some to call the use of these rhythmic words "mnenonics."

Mnemonics are used to convey rhythm in Flamenco music, for example "tumty" for 2 beats instead of "apple" and "tumpity" for 3 beats instead of "galloping" [5]. We'll revisit Flamenco in the discussion on syncopation. Generally, the rhythmic cycles of Flamenco are represented in Western music notation as combinations of more conventional time signatures such as 4/4, 6/8 and 3/4.

A very fast version of 11/16, "apple apple galloping apple apple" (2 2 3 2 2), can be heard in "Revisko Oro".

"Revisko Oro" is faster than most mortals can speak the corresponding "apple apple galloping apple apple" pattern. So how does one count off a band for this?

Another variation on the 3+2+2 rhythm is 3+3+1 as in

  • Pure Fractals 2, Vol. 2: Track 10: "Dominant Atom": 7/8 (after a few measures the 6/8 percussion pops into 7/8, 2-D musical fractal).

    A One And A Two...

    Counting these super fast beats off to start a band together is done by simply counting the accented beats only, and often 2 measures need to be counted. For example, for "Revisko Oro" the 11/16 ("apple apple galloping apple apple") count for two measures becomes a count of words with "galloping" getting 1.5 times the duration as the "apple": 
    
	1 2 3- 4 5 2 2 3- 4 5

    Here are some example tracks in 11 as 7 + 4 = 2+2+3+2+2:

    Apple Sauce

    Before we get too messy here, try playing a single note with a 5/8 rhythm to start: "apple galloping" or 2 3: "1 2 1 2 3" with the main accent on the first "1" and the secondary accent on the second "1."

    Here are some example tracks in 5:

    After getting familiar with playing combinations of 2's and 3's, adapting to new rhythms becomes much easier. And old time signatures can take on new accents more easily. For example 9/16 from a Western perspective would naturally have accents as "galloping galloping galloping", 3 3 3. However, more commonly in Macedonia this would be more interesting with syncopation such as with the "apple apple apple galloping", 2 2 2 3 rhythm found in "Olimpijski Chochek" on the "Exotic Extremes" CD and "Abdala" on the "Balkan & Beyond/Live At Costello's" CD .

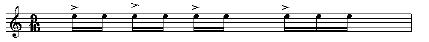
    It's not a bad idea to get used to two distinct ways of playing the 2's and 3's with a pick or finger picking. For example, with a pick, the above example of 9/16 can be played using continuous alternate picking (down, up, down, up, down, up, down, up, down, up...) or with a down stroke always on the accented first beat of the 2 or 3 note phrase. The latter method is better for consistency of accent and tone, but can limit speed more. Picking with fingernails has a parallel approach with a particular finger, say the index finger, corresponding to accented beats and other fingers corresponding to unaccented beats.

    Here are some example tracks in 9:

    Slicing The Apple

    Each basic beat (the denominator of the time signature), for example, the eighth note of 5/8 time, can of course be divided into smaller units. As mentioned above, Flamenco rhythms are also sometimes taught using mnemonics. These may be used to divide each beat. For example [5]: 
    
	1: tum
	2: (doublet): tumty
	3: (triplet): tumpity
	4: (quadruplet): tumpidity
	6: (sextuplet): rumpitytumpity
    Note the similarity to perhaps the more familiar: 
    
	1: "one" 
	2: (doublet) "one-and"
	4: (quadruple) "one-dee-and-a"
    This mnemonics technique can also be used to subdivide the beat by 5, 7 and larger numbers. For example, combine 2 and 3 for 5 subdivisions of the beat with "tumty-tumpity," and likewise for 7 with "tumty-tumty-tumpity" or 4 and 3 as in "tupidity-tumpity" and so forth. Be careful to give each syllable equal time so that the 3's don't become triplets compared to the 2's.

    Examples of large odd subdivisions of beats (and sets of beats) can be found in Brazilian drum line music, jazz, fusion and especially the music of Frank Zappa.

    Spicing The Apple

    Rhythmic ornamentations familiar to the Westerner, like trills, turns, mordents, grace notes, and slurs (bends and slides) are also used in the music of many other cultures to spice things up a bit. A notable difference in some other parts of the world, however, is the use of "accidental" notes in this ornamentation. A useful way to think of this is that rhythm gets priority over melody. In some cases, this is based on fact, sometimes not. For example, if an instrument is difficult to play a trill with an augmented second (minor third) interval, a minor second might be used instead.

    In Macedonian and Bulgarian folk music, for example, "rhythmic articulation" and rhythmic ornamentations are used without being confined to a particular scale structure or key.

    Though the unornamented melody may follow strict melodic patterns within a scale [2], the ornamentation quite often uses "accidental" notes not found in the scale of the melody. Trills and preceding grace notes used in the ornamental "rhythmic articulation" are constructing using a note a half step above the melodic note from the scale. For example, in the key of C major, a trill on C would consist of a rapid-fire repetitive alternation between C and Bb even though Bb is not in the scale. "Sitno" on Exotic Extremes is an example tune that has both these rhythmic ornamentations and mixed modes in melody.

    Similar melodic structure rule breaking for rhythmic ornamentation is found in other cultures. While concepts of harmony are not the focus of Hindustani Classical music, rules for melodic structure have been developed far beyond the Western concept of mode and scale. Check out Subtle Hint CD: Track 5: "Kedar Tease": for an electric guitar rendition of the overtone scale version of Hindustani rag "Kedar." Notes used in rhythmic ornamentation may bend these rules and often have rules of their own [1][3].

    Rhythmic ornamentation can include many subtleties in the use of slurs, pitch slides and bends, and vibrato all with particular timing, pitch range and rhythmic implications. Some are similar to bends found in jazz, rock and blues saxophone and guitar, though the pitch range, variety of pattern and extremes of modulation are much less common in these Western music genres. The use of vibrato in some Hindustani music is so extreme in modulation depth and rate as to sound as though the performer was riding a jackhammer. Ah, variety, the spice of life.

    Less Is More

    Once you get used to playing these examples, try omitting the unaccented notes while keeping the same general motion of the pick (or fingers) to help keep the rhythm naturally. Using the mechanics of your hand's physiology like a pendulum this way is a nice way to keep track of tiny slices of time for very fast, syncopated rhythms. See the Salsa examples below for an exercise in this.

    Combinations And Permutations

    Concatenation

    More complex rhythmic cycles of the Middle East, Balkans, India and other places are often constructed by combining 5's, 7's, 9's and 11's (that are themselves constructed from the 2's and 3's).

    After you get used to switching back and forth between 2's and 3's, then playing 5's, 7's and 11's, you'll be ready to play even more complex rhythmic cycles such as 35/16: 5+7+11+7+5. Here are more examples:

    Superimposition: Polyrhythms

    The rhythm section of typical traditional Salsa music is a great example of polyrhythms built from superimposing many individual rhythms, each of which may be thought of as built from 2's and 3's. While the time signatures are more familiar such as 4/4, the mix of straight and syncopated rhythms creates an overall complex rhythm.

    One earlier example was "Sitno" which is a Bulgarian tune with superimposed 3/4, 6/8, and 2/4. Some of the more interesting rhythms from Ghana, are played and/or sung by having different people in different time signatures or rhythmic cycles. An ode to the diety "Boka" includes 7/4 played over 3/4. This creates a rhythmic cycle with a pattern that repeats after 21 beats, the least common multiple of 3 and 7.

    In addition to Balkan and African examples above, there are many other cultures with tunes using one time signature played over another: Traditional and contemporary (ala Steve Morse) Celtic tunes, Brazilian drum line music, jazz and other traditions also have examples. An original tune I've played in concert many times in the last couple of years (sorry, the recording is pending the release of my third album) overlaps 4/4 and 6/8, with the lower register of the guitar playing 6/8 notes in the bass-line while the upper register plays 4/4.

    Ah, but how would you play the two parts on a guitar? One way is to think of the two parts as a whole, which then generally becomes a more syncopated rhythm with a more complex time signature. So lets look at syncopation before we go any further.

    Again, an example of this is a continuous 12/8 section playing along with

  • Subtle Hint: Track 19: "So Much For Justice": 48 as 4 x 12 as 5 (=2+3) + 7 (=2+2+3) + 4+4+4 + 5 (=2+3) + 7 (=2+2+3) + 3+3+3+3

    Syncopation: Divide And Conquer

    After one has mastered the 2's and 3's, playing any time signature or combination thereof becomes easier. Any rhythmic cycle can be constructed using this method.

    Ravi Shankar's "My Music, My Life" [1] has many exercises with combinations and permutations of these, including those in "teen tal" which is a rhythmic cycle of 16 beats. At first you might say to yourself "Hey, there are 16 16th notes in 4/4, so what's the big deal?" The rhythms in the exercises are actually quite syncopated as in "2-3-2-3-3-3" and "3-3-2-2-3-3."

    When you encounter syncopated rhythms for the first time, either listening or reading Western music notation, deconstruction into 2's and 3's (apples and gallopings) can be useful even for simpler, more familiar time signatures.

    Salsa Syncopation Example

    The most important rhythm in the highly syncopated Salsa music tradition is the "Clave" rhythm named after the percussion instrument that normally plays it. Claves are two sticklike cylinders of hard material. When struck together, they make a high-pitched piercing pulse. The pulse is so short in time, so staccato, that it is extremely effective as a precise reference in time.

    Typically, only the accents are heard played on claves:

    In terms of our apples and gallopings, the "son clave" rhythm is 

    
	"galloping galloping apple (apple) apple apple (apple)": 3 3 2 (2) 2 2 (2),

    where "()" denotes rest. From here, delete the unaccented beats and you end up with the rhythm shown by the conventional music notation above.

    You might also recognize this as a rock guitar rhythm from tunes like "Who Do You Love" by George Thorogood & The Destroyers.

    Notice that there are 3 accents, corresponding to 3 words before the first rest: "galloping galloping apple": 3 3 2. Then 2 accents, corresponding to two words: "apple apple": 2 2. For Salsa players, this clave rhythm is known as "three two" clave, as opposed to "two three" clave [4]. "Two three" clave swaps the 2 and 3 accent phrases: 

    	
	"(apple) apple apple (apple) galloping galloping apple": (2) 2 2 (2) 3 3 2

    Flamenco Syncopation Example

    Flamenco rhythms include hemiola, in which rhythmic time values are in relationship of 3/2. An example of this relationship comes from the Bulerias rhythm of the 3/4, 6/8 Flamenco "compas" (rhythmic cycle) families [5].

    This example includes a 6/8 question (Q) and a 3/4 answer (A):

    Grouping in 2's and 3's and using corresponding mnemonics: 

    	
	Q: 3 3 ("tumpity tumpity" or "galloping galloping")
	A: 2 2 2 ("tumty tumty tumty" or if you prefer "apple apple apple")
    Compare to the hemiola rhythm associated with the lyric "I want to be an A-mer-i-can" from "West Side Story."

    Although this example might seem trivial, it nonetheless illustrates the method that can be applied to more complex written and heard music. The 3+3 and 2+2+2 rhythms mentioned hear are analogous to the 3+3+3+3 and 4+4+4 rhythms embedded in

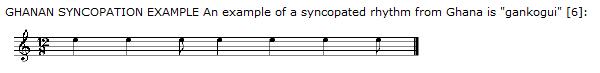
  • Balkan & Beyond/Live At Costello's: Track 9: Meshano Oro (64 beat tune: 3+2+2+3+2+2+2+3+2+2+3+3+3+2+3+2+3+3+3+2+3+2+3+2+2+2)

    Ghanan Syncopation Example

    It has a 12 beat rhythmic cycle of 2 2 1 2 2 2 1 which can also be represented a 2 3 2 2 3 with only the primary and secondary accents played: Since the secondary accents of the 3 beats are on the 3rd beat, this corresponds to starting with: 

    	
	"apple galloping apple apple galloping"
    and dropping the unaccented syllables: 
    	
	"ap - gal - ping ap - ap - gal - ping"
    Note that the 2 2 1 2 2 2 1 rhythm has only a subtle difference from (and my be substitued with) 2 3 2 2 3 mentioned above for

    Polyrhythms As A Single Syncopated Rhythm: Example

    Each of the syncopation examples above, from Salsa, Flamenco and Ghana, is an isolated syncopated rhythm that is normally played against other rhythms to form a polyrhythm. An approach to playing these parts well in an ensemble is to understand how each of these individual syncopated rhythms fit into the whole of the associated polyrhythm.

    And this brings us back to the question of how to play things like 4/4 and 6/8 simultaneously. One approach is to acknowledge that there are two meters occurring simultaneously, and to count one while playing the other [7]. I find a more useful approach, at least to start, is to convert the two meters into one instead. To convert the two into one meter, determine a least common multiple of time signature numerators, determine all of the accents, and convert the rhythm into 2's and 3's, or larger familiar numbers if appropriate.

    For example, for 4/4 over 6/8, the time signature numerators are 4 and 6. The least common multiple is 12 (4x3 =12, 2x6 = 12). Now, describing the 4/4 beats in terms of 12/8: 

    	
	"galloping galloping galloping galloping" or 3 3 3 3.
    And as is conventional for 4/4 time, accents are as follows: 
    	
	- primary accent on the 1st 4/4 beat (P) and 
	- secondary on the 3rd 4/4 beat (S), 
	- tertiary accent on the 2bd 4/4 beat (T) and
	- unaccented beat on the 4th 4/4 beat (X).
    Now, multiplying 4 by 3 to get 12, the accents become: 
    	
	1  2  3  4  5  6  7  8  9 10 11 12
 	P  -  -  T  -  -  S  -  -  X  -  -
    And for 6/8, 
    
	"apple apple apple apple apple apple": 2 2 2 2 2 2:
    The primary accent is on the very first 6/8 beat (P) and the secondary on the forth 6/8 beat (S), the tertiary accent on the third 6/8 beat and the unaccented beats are in between (X). Now, multiplying 6 by 2 to get 12, the accents become: 
    	
	1  2  3  4  5  6  7  8  9 10 11 12
 	P  -  X  -  T  -  S  -  X  -  T  -
    Now put accents together into one using the rule that stronger accents win: 
    	      1  2  3  4  5  6  7  8  9 10 11 12
 	4/4:	 P  -  -  T  -  -  S  -  -  X  -  -
 	6/8:	 P  -  X  -  T  -  S  -  X  -  T  -
  
        both:    P  -  X  T  T  -  S  -  X  X  T  -
    To give you a general feel for this rhythm, if you were to treat all accents equally, you'd get: 
    
	 1  2  3  4  5  6  7  8  9 10 11 12
 	 X  -  X  X  X  -  X  -  X  X  X  -
    This rhythm corresponds to rhythm of the main melody of "Carol of The Bells."

    Finally, to play a tune with 4/4 on 6/8, the two can be put together in 12/8 or 12/16 time and accents dealt with as shown above.

    Going A "Step" Further

    If you'd like to go beyond the rhythmic training one gets from all these exercises on guitar, listening to music such as the examples on my CD, reading more from materials such as the references below, learn to dance some of the traditional dances that go with the music. Having the total body kinesthetic experience of the rhythm is a great way to solidify all the technical information in your brain.

    There You Go...

    Building rhythms from groups of 2 and 3 beats, along the associated mnemonics, can be a great tool for understanding, internalizing, creating, playing written and improvised parts with complex time signatures, syncopation and superimposed polyrhytms.

    References

    [1] Bor, Joep, "The Raga Guide: A Survey of 74 Hindustani Ragas," Nimus Records, 1999.

[2] Rice, Timothy, "May It Fill Your Soul," University Of Chicago Press, 1994.

[3] Shankar, Ravi, "My Music, My Life," Simon and Schuster, New York, 1968.

[4] Gerard, Charley, "Salsa! The Rhythm of Latin Music," White Cliffs Media, Tempe AZ, 1998, p. 33-34.

[5] Keyser, "Flamenco Chuck," "Introduction To Flamenco: Rhythmic Foundation and Accompaniement,"
	http://users.aol.com/CHKeyser/private/compas/Analysis.pdf

[6] Montfort, Matthew, "Ancient Traditions -- Future Possibilities: Rhythmic Training Through the Traditions of Africa, Bali and India." Mill Valley: Panoramic Press, 1985.

[7] Magadini, Peter, "Polyrhythms - The Musician's Guide" Hall Leonard Corporation, Tempe AZ, 1993, p. 2.

    Kevin Ferguson is a Portland, Oregon based guitarist, engineer, scientist, inventor with several albums and dozens of patents. See his homepage for more articles on music, example audio and video recordings of his performances of these using many of the rhythms described above and music videos, inventions and more.

    Additional Columns by Kevin Ferguson

    EXOTIC EXTREMES DIGITAL DOWNLOAD

    "BEAUTY IN YOUR HEAD" (released July 4, 2019) DIGITAL DOWNLOAD: